Balanced Binary Tree
Given a binary tree, determine if it is height-balanced. A height-balanced binary tree is a binary tree in which the depth of the two subtrees of every node never differs by more than one.
Problem Statement
LeetCode-110: Given a binary tree, determine if it is height-balanced. A height-balanced binary tree is a binary tree in which the depth of the two subtrees of every node never differs by more than one.
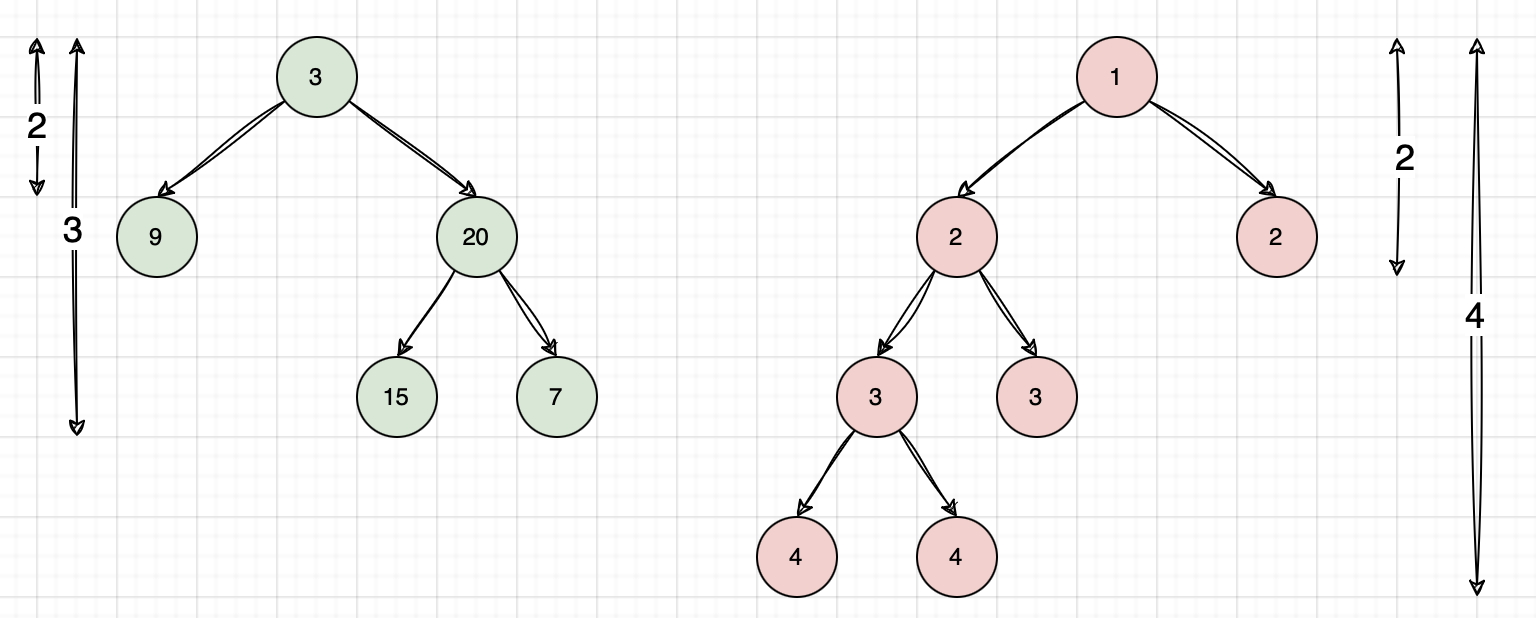
Balanced Binary Tree
Approach
Based on the definition of a height balanced binary tree, following is a high level approach to solve this problem:
- Calculate height of left and right subtree at every level.
- For every level, check if the difference of the heights of the left and right subtree is more than 1.
- If the difference is more than 1, the tree is NOT a height balanced binary tree.
Implementation
Here is a java implementation of the above mentioned approach:
public boolean isBalanced(TreeNode root) {
if(null == root){
return true;
}
// Calculate height of left and right subtree
int left = height(root.left);
int right = height(root.right);
// Check if the difference of heights is more than 1
return Math.abs(left-right) <= 1 &&
isBalanced(root.left) &&
isBalanced(root.right);
}
private int height(TreeNode node){
if(null == node){
return 0;
}
return 1+ Math.max(height(node.left), height(node.right));
}
The above mentioned approach works but is not optimal. The approach taken invokes the height method for every recursive call of the isBalanced method, leading to redundant calculations.
We can optimize the above approach by keeping a track of the maximum difference of the left and right subtree heights at every level. If the maximum difference of left and right subtree heights at any level is more than 1, the tree is NOT a height balanced binary tree.
- Keep track of the maximum difference of the left and right subtree heights at every level.
- Once all the nodes are visited, if the maximum difference of left and right subtrees at any level is more than 1, the tree is NOT a height balanced binary tree.
Here is the updated approach:
private int maxHeightDifference = Integer.MIN_VALUE;
public boolean isBalanced(TreeNode root) {
if(null == root){
return true;
}
calculateHeightDifferenceViaDFS(root);
return maxHeightDifference <= 1;
}
private int calculateHeightDifferenceViaDFS(TreeNode root){
if(null == root){
return 0;
}
int left = calculateHeightDifference(root.left);
int right = calculateHeightDifference(root.right);
maxHeightDifference = Math.max(maxHeightDifference, Math.abs(left-right));
return 1 + Math.max(left, right);
}
Complexity Analysis
As each node of the tree is processed once, the overall complexity of this algorithm is \(O(n)\) where \(n\) is the number of nodes in the tree.