Coin Change
You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money. Return the fewest number of coins that you need to make up that amount.
Problem Statement
LeetCode-322: You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.
Return the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.
You may assume that you have an infinite number of each kind of coin.
Approach
Let’s try to solve this problem using a recursive DFS method. On a high level, we can think of this problem as a tree traversal problem where each node represents the remaining amount of money to be made up. The children of a node represent the possible coins that can be used to make up the remaining amount.
- We start with the initial amount
amountand recursively try to make up the remaining amount by using each coin in thecoinsarray. - If the remaining amount is less than 0, we return
-1as it is not possible to make up the remaining amount. - If the remaining amount is 0, we return
0as we have successfully made up the amount. - If the remaining amount is greater than 0, we recursively try to make up the remaining amount by using each coin in the
coinsarray. - We keep track of the minimum number of coins required to make up the amount and return the minimum number of coins required.
Let’s implement the above approach.
public int coinChange(int[] coins, int amount) {
return dfs(coins, amount);
}
private int dfs(int[] coins, int amount) {
if (amount < 0) {
return -1;
}
if (amount == 0) {
return 0;
}
int minCoins = Integer.MAX_VALUE;
for (int coin : coins) {
int res = dfs(coins, amount - coin);
if (res >= 0) {
minCoins = Math.min(minCoins, res + 1);
}
}
return minCoins == Integer.MAX_VALUE ? -1 : minCoins;
}
But this approach is not efficient as we are solving the same subproblems multiple times. Consider the following example:
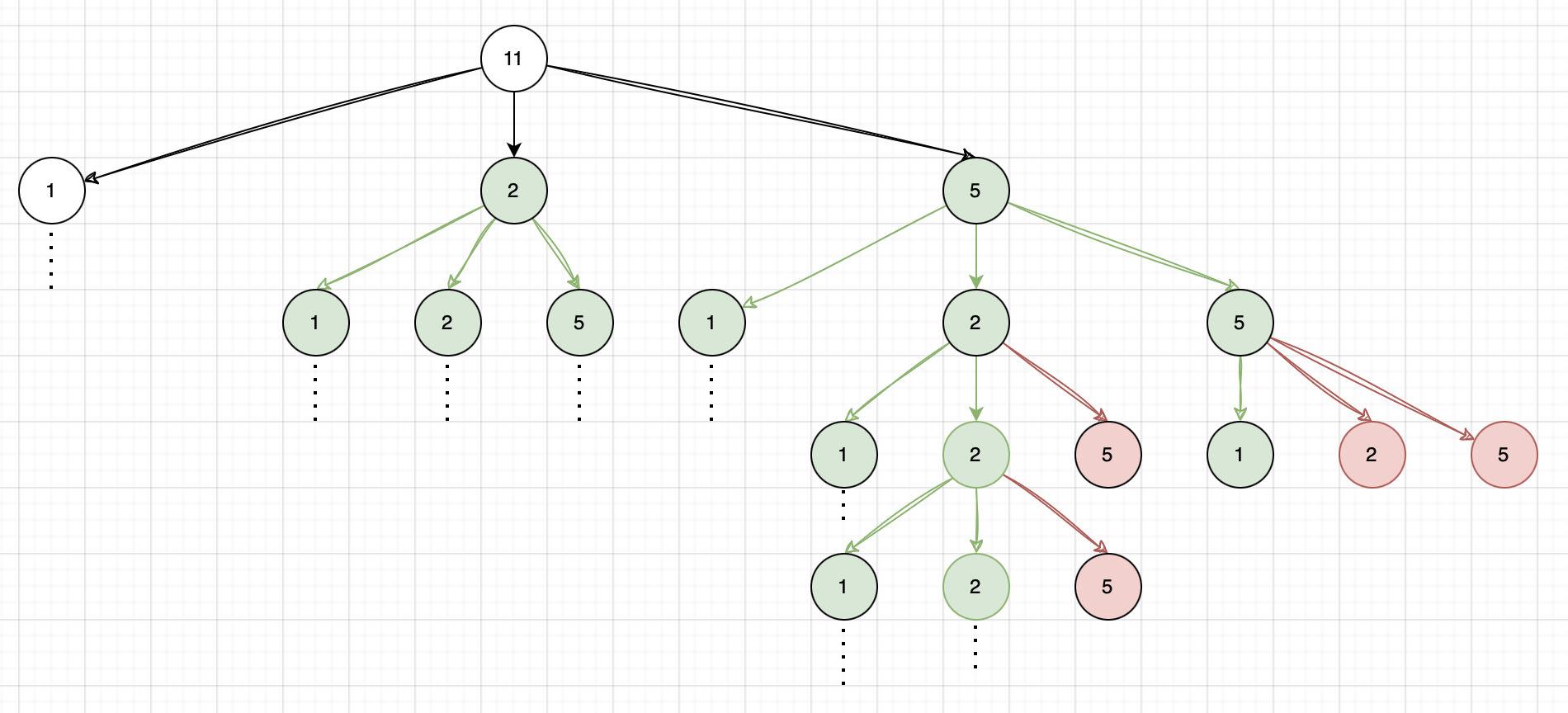
Amount=11; coins[] = {1, 2, 5}
As we can see in the illustration above, we are solving the multiple subproblems repeatedly; for example, the subproblem dfs(2) is solved 75 times and the subproblem dfs(1) is solved 128 times. This clearly indicates the inefficiency of the recursive DFS approach.
To overcome this inefficiency, we can use dynamic programming to store the results of the subproblems and reuse them when needed. We can use a 1D array dp[] to store the minimum number of coins required to make up the amount i. We initialize the dp[] array with a value greater than the maximum amount possible, i.e., amount + 1.
- We initialize the
dp[0]with0as the minimum number of coins required to make up the amount0is0. - For each amount
ifrom1toamount, we try to make up the amountiby using each coin in thecoinsarray. - We update the
dp[i]with the minimum number of coins required to make up the amounti. - Finally, we return the value of
dp[amount]if it is less than or equal toamount, else we return-1.
Implementation
Here is a Java implementation of the above approach:
public int coinChangeV2(int[] coins, int amount) {
// We use an array to save the results of the subproblems. dp[i] will be storing
// the minimum number of coins required for i value. So dp[amount] will have result.
int max = amount + 1;
int[] dp = new int[amount + 1];
// Initialize all dp[i>0] values as maximum.
Arrays.fill(dp, max);
// This is a base case, to make the amount 0, no coin will be needed.
dp[0] = 0;
// loop through every value from 1 to the desired amount,
// attempting to subtract each coin value.
// If a coin value can be subtracted (i.e., is not larger
// than the current amount being considered), it checks if
// subtracting this coin leads to a smaller number of coins needed
// than the current stored value, and updates its value if it does.
// It returns the final dp value for the desired amount, or -1
// if it's equal to the placeholder value (i.e., no valid combination
// was found).
// If a combination was found which sums to the amount,
// it will definitely have a value less than or equal to amount,
// hence dp[amount] > amount indicates no valid combination.
for (int currAmount = 1; currAmount <= amount; currAmount++) {
// for every coin in the array
for (int j = 0; j < coins.length; j++) {
// if current denomination is less than or equal to the current amount
// we can use it to make up the current amount
if (coins[j] <= currAmount) {
int remainingAmount = currAmount - coins[j];
dp[currAmount] = Math.min(dp[currAmount], dp[remainingAmount] + 1);
}
}
}
// If dp[amount] > amount, there are no combinations that sum to amount.
return dp[amount] > amount ? -1 : dp[amount];
}
Complexity Analysis
The time complexity of the above approach is O(amount * n), where n is the number of coins and amount is the total amount of money. We are iterating through each amount from 1 to amount and for each amount, we are iterating through each coin in the coins array.