Flood Fill

Problem Statement

LeetCode-733: An image is represented by an m x n integer grid image where image[i][j] represents the pixel value of the image.

You are also given three integers sr, sc, and color. You should perform a flood fill on the image starting from the pixel image[sr][sc].

To perform a flood fill, consider the starting pixel, plus any pixels connected 4-directionally to the starting pixel of the same color as the starting pixel, plus any pixels connected 4-directionally to those pixels (also with the same color), and so on. Replace the color of all of the aforementioned pixels with color.

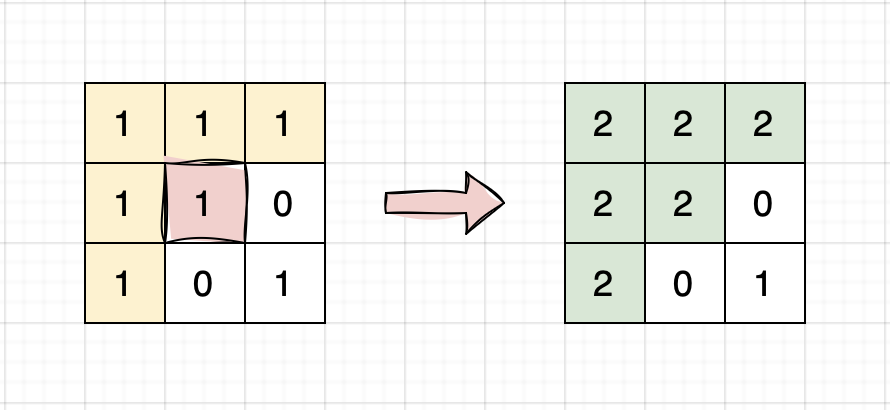
Return the modified image after performing the flood fill.

Approach

We are give a starting pixel color, let’s call it curr. The ask is to color all the adjacent pixels in 4 directions only if their color is equal to curr.

We can use a recursive DFS algorithm to traverse the grid where the base case will be:

1. Current row and col is out of bound.
2. The current pixel color is not curr.

Implementation

Here is a java implementation of the DFS approach:

private final int[] dirs = new int[] { 1, 0, -1, 0, 1 };
public int[][] floodFill(int[][] image, int sr, int sc, int color) {
    solve(image, sr, sc, color, image[sr][sc]);
    return image;
}x
private void solve(int[][] image, int sr, int sc, int color, int curr) {
    if (!isValid(image, sr, sc, color) || image[sr][sc] != curr) {
        return;
    }
    image[sr][sc] = color;
    for (int i = 0; i < dirs.length - 1; i++) {
        solve(image, sr + dirs[i], sc + dirs[i + 1], color, curr);
    }
}
private boolean isValid(int[][] image, int row, int col, int color) {
    int rows = image.length;
    int cols = image[0].length;
    return row >= 0 && row < rows &&
            col >= 0 && col < cols &&
            image[row][col] != color;
}

Complexity Analysis

As all the pixels in the image are potential candidates, we might end up processing all the pixels, so the overall time complexity is \(O(n)\).

Similarly, the recursive stack due to DFS also contributes \(O(n)\) to the space complexity.