Implement Queue Using Stacks

Problem Statement

LeetCode-232: Implement a first in first out (FIFO) queue using only two stacks. The implemented queue should support all the functions of a normal queue (push, peek, pop, and empty).

Implement the MyQueue class:

• void push(int x): Pushes element x to the back of the queue.
• int pop(): Removes the element from the front of the queue and returns it.
• int peek(): Returns the element at the front of the queue.
• boolean empty(): Returns true if the queue is empty, false otherwise.

Notes:

• You must use only standard operations of a stack, which means only push to top, peek/pop from top, size, and is empty operations are valid.
• Depending on your language, the stack may not be supported natively. You may simulate a stack using a list or deque (double-ended queue) as long as you use only a stack’s standard operations.

Approach

Before jumping into the solution, let us first recall the difference between two data structures:

• Queue: is a FIFO(first-in-first-out) data structure where the insertion and deletion of elements happen at two far ends (head and tail).
• Stack: on the other hand is a LIFO(last-in-first-out) data structure where the insertion and deletion of elements happen at the same end i.e. head.

To implement a queue using two stacks, we need to simulate a FIFO behavior using two data structures of LIFO nature. There are two approaches to achieve the same.

Using a single stack for both push and pop

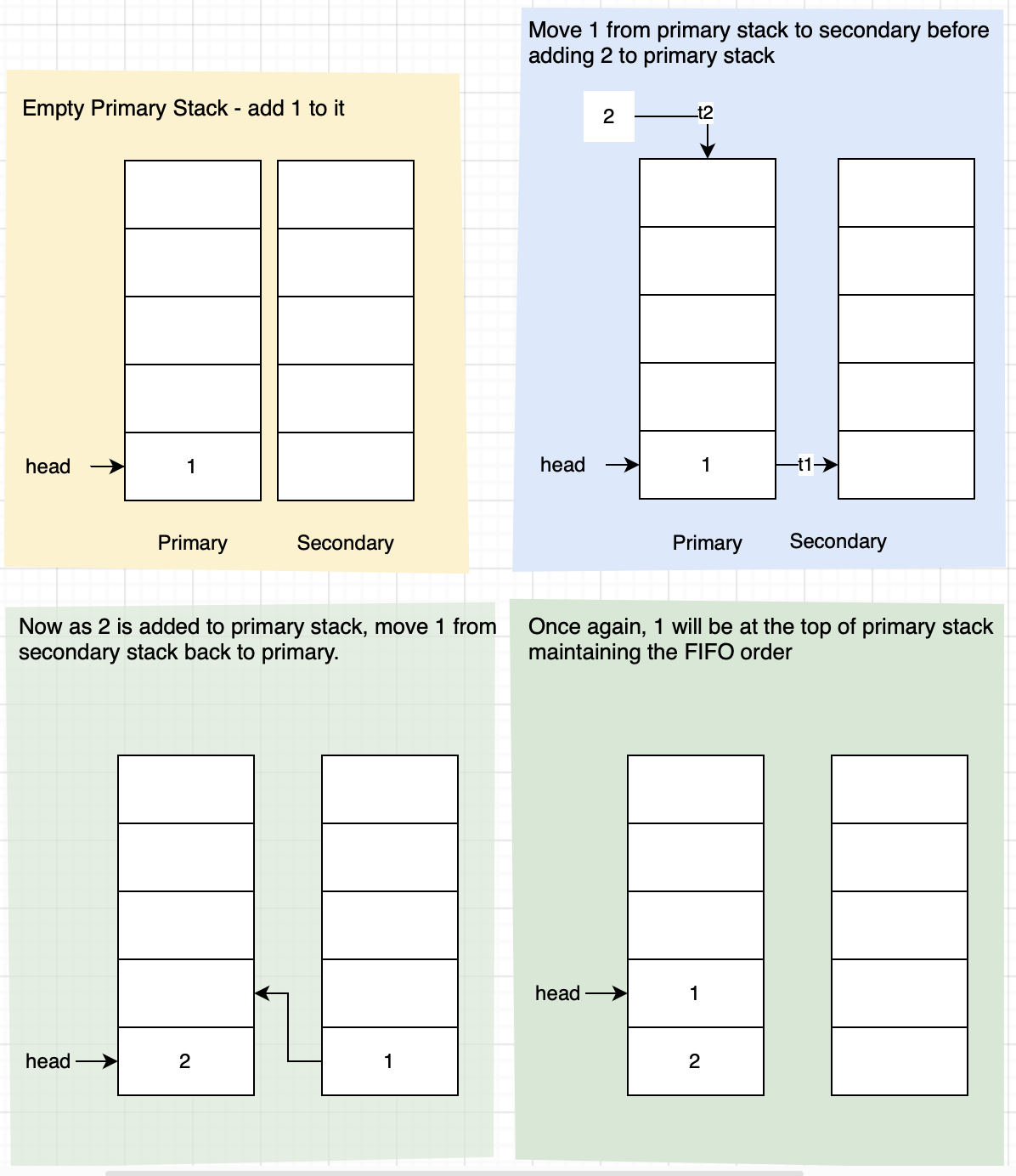
The overall idea is to maintain the order of elements in the stack by moving the elements from the primary stack to the secondary stack and vice-versa. This will help us to achieve the FIFO behavior of the queue.

1. Push: For pushing an element, we will first move all the elements from the primary stack to the secondary stack. This will help us to maintain the order of elements in the stack. Then we will push the new element to the primary stack. Finally, we will move all the elements from the secondary stack back to the primary stack.
2. Pop: For popping an element, we will simply pop the top element from the primary stack.
3. Peek: For peeking an element, we will simply peek the top element from the primary stack.
4. Empty: For checking if the queue is empty, we will check if the primary stack is empty.

Complexity Analysis: As we are moving all the elements already pushed to the primary stack on every push method call, the time complexity for the push operation is \(O(n)\) and for the pop, peek, and empty operations is \(O(1)\)

class MyQueue {
    private final Stack<Integer> primary;
    private final Stack<Integer> secondary;

    public MyQueue() {
        primary = new Stack<>();
        secondary = new Stack<>();
    }
    
    public void push(int x) {
        while(!primary.isEmpty()){
            secondary.push(primary.pop());
        }
        primary.push(x);
        while(!secondary.isEmpty()){
            primary.push(secondary.pop());
        }
    }
    
    public int pop() {
        return primary.pop();
    }
    
    public int peek() {
        return primary.peek();
    }
    
    public boolean empty() {
        return primary.isEmpty();
    }
}

Using two stacks for push and pop

In this approach, we will use two stacks - one for pushing the elements and the other for popping the elements. The primary stack will be used for pushing the elements and the secondary stack will be used for popping the elements.

The steps for the operations are as follows:

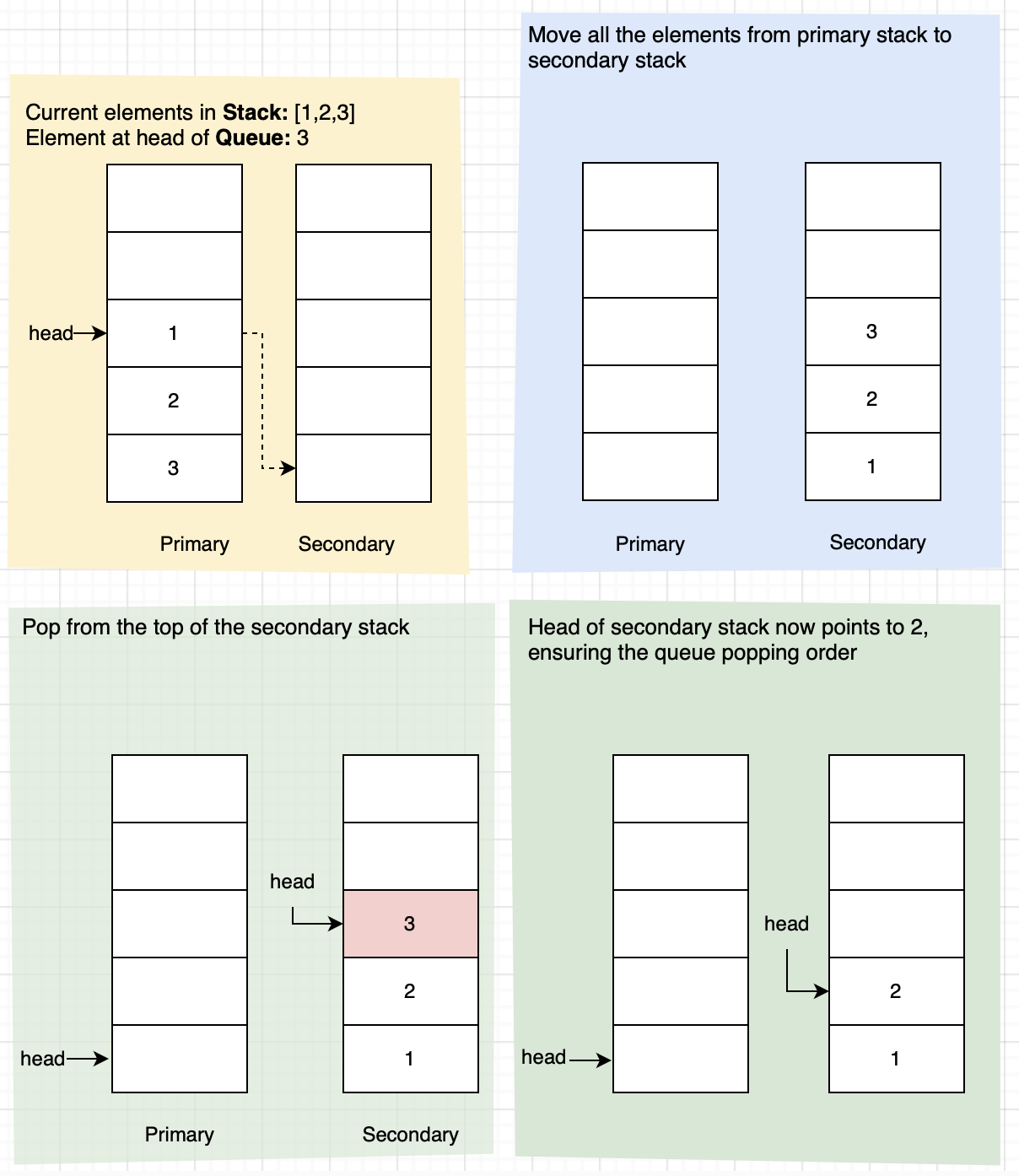
1. Push: For pushing an element, we will simply push the element to the primary stack.
2. Pop: For popping an element, we will first check if the secondary stack is empty. If it is empty, we will move all the elements from the primary stack to the secondary stack. Then we will pop the top element from the secondary stack.
3. Peek: For peeking an element, we will first check if the secondary stack is empty. If it is empty, we will move all the elements from the primary stack to the secondary stack. Then we will peek the top element from the secondary stack.
4. Empty: For checking if the queue is empty, we will check if both the primary and secondary stacks are empty.

Complexity Analysis: The time complexity for the push and empty operations is \(O(1)\) and for the pop, peek, operations, it is \(O(n)\).

But if we look at the amortized time complexity, the time complexity for the pop and peek operations is \(O(1)\) as we are moving the elements from the primary stack to the secondary stack only when the secondary stack is empty.

The worst-case time complexity for the pop and peek operations is \(O(n)\) only when the secondary stack is empty which happens only once for every \(n\) elements pushed to the primary stack.

class MyQueue {
    private final Stack<Integer> primary;
    private final Stack<Integer> secondary;

    public MyQueue() {
        primary = new Stack<>();
        secondary = new Stack<>();
    }
    
    public void push(int x) {
        primary.push(x);
    }
    
    public int pop() {
        if(secondary.isEmpty()){
            while(!primary.isEmpty()){
                secondary.push(primary.pop());
            }
        }
        return secondary.pop();
    }
    
    public int peek() {
        if(secondary.isEmpty()){
            while(!primary.isEmpty()){
                secondary.push(primary.pop());
            }
        }
        return secondary.peek();
    }
    
    public boolean empty() {
        return primary.isEmpty() && secondary.isEmpty();
    }
}