Insert Interval
Insert newInterval into intervals such that intervals is still sorted in ascending order by start and intervals still does not have any overlapping intervals (merge overlapping intervals if necessary).
Problem Statement
LeetCode-57: You are given an array of non-overlapping intervals where $intervals[i] = [start_i \ , end_i]$ represent the start and the end of the $i^{th}$ interval and intervals is sorted in ascending order by $start_i$.
You are also given an interval newInterval = [start, end] that represents the start and end of another interval.
Insert newInterval into intervals such that intervals is still sorted in ascending order by $start_i$ and intervals still does not have any overlapping intervals (merge overlapping intervals if necessary). Return intervals after the insertion.
Input: intervals = [[1,3],[6,9]], newInterval = [2,5]
Output: [[1,5],[6,9]]
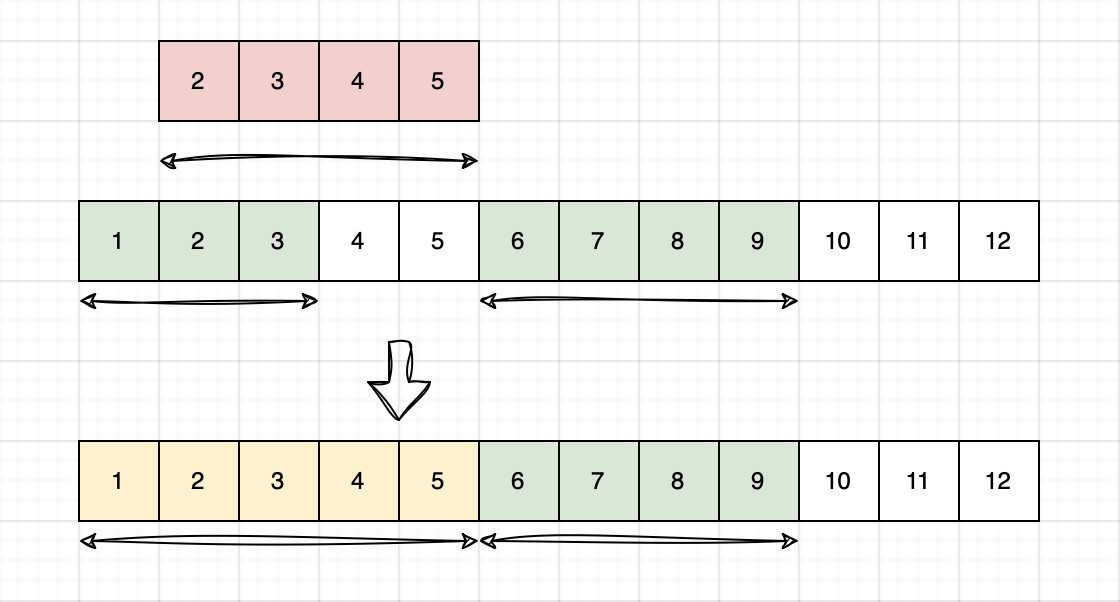
Merge Overlapping Intervals
Another example (Note that you don’t need to modify intervals in-place. You can make a new array and return it.):
Input: intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
Output: [[1,2],[3,10],[12,16]]
Explanation: Because the new interval [4,8] overlaps with [3,5],[6,7],[8,10].
Approach
While iterating over the intervals, we need to consider the following three cases for each interval (current):
- The newInterval is before the current interval: If the
newIntervalis before the current interval, we can add the newInterval to the result and update the newInterval to the current interval. - The newInterval is after the current interval: If the
newIntervalis after the current interval, we can add the current interval to the result. - The newInterval overlaps with the current interval: If the
newIntervaloverlaps with the current interval, we can merge the newInterval with the current interval and update the newInterval.
Implementation
Here is a Java implementation of the above approach:
public int[][] insert(int[][] intervals, int[] newInterval) {
List<int[]> res = new ArrayList<>();
for(int i=0; i < intervals.length; i++){
int[] curr = intervals[i];
// case-1: if newInterval is to the left
// of current interval
if(newInterval[1] < curr[0]){
res.add(newInterval);
newInterval = curr;
}
// case-2: if newInterval is to the right
// of current interval
else if(newInterval[0] > curr[1]){
res.add(curr);
}
// case-3: if newInterval overlaps with
// current interval
else{
newInterval[0] = Math.min(newInterval[0], curr[0]);
newInterval[1] = Math.max(newInterval[1], curr[1]);
}
}
// add the last interval
res.add(newInterval);
return res.toArray(new int[0][0]);
}
Complexity Analysis
The time complexity for this approach is $O(N)$, where $N$ is the number of intervals in the input array. We iterate over all the intervals once.
Follow-up
Let us re-consider the first scenario:
If the
newIntervalis before the current interval, we can add the newInterval to the result and update the newInterval to the current interval.
As the input intervals are already non-overlapping, in case the newInterval is before the current interval, we can directly add the newInterval to the result and add rest of the intervals as it is. This is because if the newInterval is before the current interval, it will also be before all the remaining intervals - which are already given to be sorted and non-overlapping.
public int[][] insert(int[][] intervals, int[] newInterval) {
List<int[]> res = new ArrayList<>();
for(int i=0; i < intervals.length; i++){
int[] curr = intervals[i];
// case-1: if newInterval is to the left
// add newInterval and rest of the intervals
if(newInterval[1] < curr[0]){
res.add(newInterval);
while(i < intervals.length){
res.add(intervals[i]);
i++;
}
return res.toArray(new int[0][0]);
}
// case-2: if newInterval is to the right
// of current interval
if(newInterval[0] > curr[1]){
res.add(curr);
}
// case-3: if newInterval overlaps with
// current interval
else{
newInterval[0] = Math.min(newInterval[0], curr[0]);
newInterval[1] = Math.max(newInterval[1], curr[1]);
}
}
res.add(newInterval);
return res.toArray(new int[0][0]);
}
The time complexity for this approach is also $O(N)$, as we are still iterating over all the intervals once. A slightly modified version of the same approach is implemented below:
public int[][] insert(int[][] intervals, int[] newInterval) {
List<int[]> result = new ArrayList<>();
int i = 0, n = intervals.length;
// add all intervals before newInterval
while (i < n && intervals[i][1] < newInterval[0]) {
result.add(intervals[i]);
i++;
}
// merge overlapping intervals
while (i < n && intervals[i][0] <= newInterval[1]) {
newInterval[0] = Math.min(newInterval[0], intervals[i][0]);
newInterval[1] = Math.max(newInterval[1], intervals[i][1]);
i++;
}
result.add(newInterval);
// add remaining intervals
while (i < n) {
result.add(intervals[i]);
i++;
}
return result.toArray(new int[0][]);
}