Lowest Common Ancestor of a Binary Search Tree
Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.
Problem Statement
LeetCode-235 : Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
Approach
Here are a few observations:
- The nodes
pandqare given to be always present, which means we can skip a couple of edge cases. - No duplicate values, the comparison operators do not need an \(==\) comparison.
- Being a BST, the nodes p and q will follow the principle of position i.e. if \(p.val < root.val \); p will be in the left subtree of root, and in right subtree otherwise (values given to be unique).
Based on these observations, following is an algorithm to work with:
While traversing the tree:
- If both
pandqare greater than therootnode’s value, it means both nodes are in the right subtree. So, move to the right subtree of therootnode. - If both
pandqare less than the current node’s value, it means both nodes are in the left subtree. So, move to the left subtree of therootnode. - If one of
porqis on one side and the other is on the other side, or if one of them is equal to the current node, then the current node is the LCA.
Note: one of them is equal to the current node \( \Rightarrow \) Consider the following illustration, for nodes 2 and 4, during tree traversal, when root is pointing to 2, it is equal to the p.val.
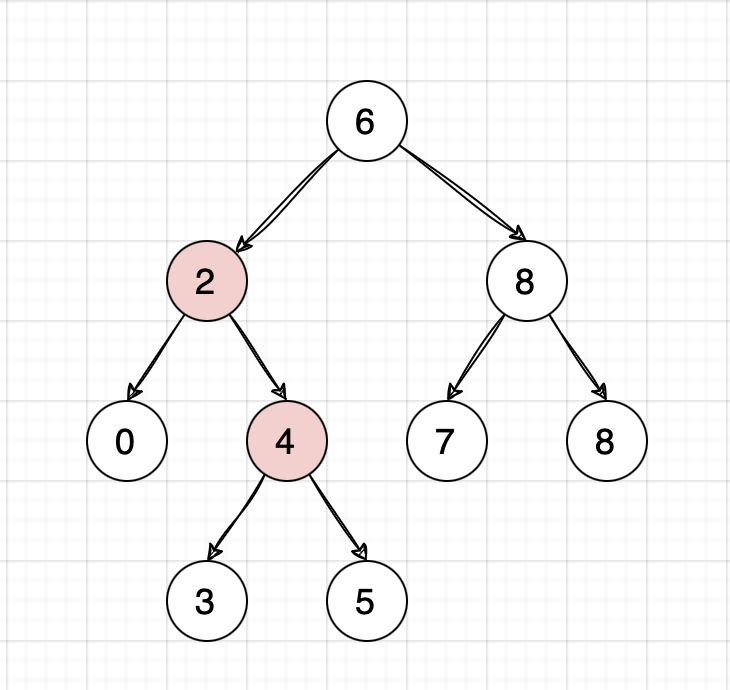
Lowest Common Ancestor
Implementation
Following is a java implementation of the above mentioned approach:
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q){
// both the nodes less than the root value
// move to left subtree
if(p.val < root.val && q.val < root.val){
return lowestCommonAncestor(root.left, p, q);
}
// both the nodes greater than the root value
// move to left subtree
else if(p.val > root.val && q.val > root.val){
return lowestCommonAncestor(root.right, p, q);
}
// nodes are in separate subtrees
// or while traversing we have now
// reached at a stage where either of the nodes is equal
// to current root
return root;
}
Complexity Analysis
This algorithm finds the LCA in \(O(h)\) time, where h is the height of the BST.