Symmetric Tree
Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).
Problem Statement
LeetCode-101: Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).
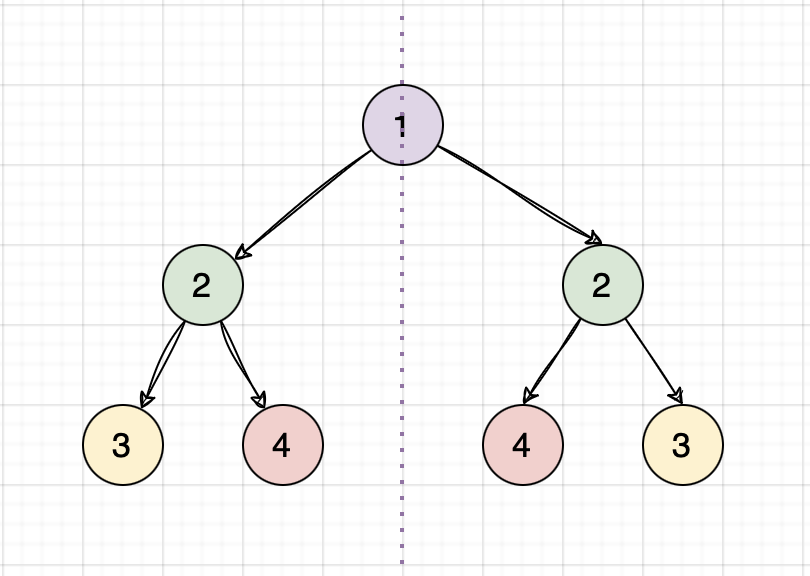
Symmetrical Tree
Approach
The problem can be solved using a recursive approach. The idea is to check if the left subtree of the root is a mirror of the right subtree of the root.
To check if two trees are a mirror of each other:
- If either of the trees is
null, then both trees should benull. - Check if the values of the root nodes of both trees are equal.
- Check if the right subtree of the left tree is a mirror of the left subtree of the right tree.
- Check if the left subtree of the left tree is a mirror of the right subtree of the right tree.
Implementation
Here is a java implementation of the above approach:
public boolean isSymmetric(TreeNode root) {
if(null == root){
return true;
}
return check(root.left, root.right);
}
private boolean check(TreeNode left, TreeNode right){
if(null == left || null == right){
return null == left && null == right;
}
return left.val == right.val
&& check(left.left, right.right)
&& check(left.right, right.left);
}
Complexity Analysis
The time complexity for this approach is $O(N)$, where $N$ is the number of nodes in the binary tree. The space complexity is $O(N)$ as well, considering the recursive stack space.
Follow-up
Can we solve the problem iteratively?
We can use a queue to traverse the tree level by level. At each level, we check if the nodes are symmetric. If they are, we add the left and right children of the nodes to the queue.
Note that we need to ensure that the nodes are added in the correct order:
- The
leftchild of theleftnode should be compared with therightchild of therightnode, - and the
rightchild of theleftnode should be compared with theleftchild of therightnode.
Here is the iterative implementation:
public boolean isSymmetric(TreeNode root) {
if(null == root || (null == root.left && null == root.right)){
return true;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root.left);
queue.add(root.right);
while(!queue.isEmpty()){
TreeNode left = queue.remove();
TreeNode right = queue.remove();
// leaf node
if(null == left && null == right){
continue;
}
// one of the nodes is null
// or the values are not equal
else if(null == left || null == right || left.val != right.val){
return false;
}
queue.add(left.left);
queue.add(right.right);
queue.add(left.right);
queue.add(right.left);
}
return true;
}